心理统计学历年考研试题集锦

• 第一章 绪论
• 第二章 统计图表
• 第三章 集中量数
• 第四章 差异量数
• 第五章 相关关系
• 第六章 概率分布
• 第七章 参数估计
• 第八章 假设检验
• 第九章 方差分析
• 第十章 卡方检验
• 第十一章 非参数检验
• 第十二章 线性回归
• 第十三章 多变量统计分析简介
• 第十四章 抽样原理及方法

第一章 绪论

概念题

1. 描述统计 (吉林大学2002研)
2. 推论统计(中国政法大学2005研，浙大2000研)
3. 假设检验 (浙大2002研)

选择题

1. 等距量表的特点是（ ）。（统考2007研）
   A. 无绝对零点，无相同单位
   B. 无绝对零点，有相同单位
   C. 有绝对零点，无相同单位
   D. 有绝对零点，有相同单位
2. 下列量表中，具有绝对零点的是（ ）。（统考2008研）
   A. 称名量表
   B. 顺序量表
   C. 等距量表
   D. 比率量表

第二章 统计图表

选择题

1. 用于描述两个变量之间的相关关系的统计图是（ ）。（统考2007研）
   A. 直方图
   B. 线性图
   C. 条形图
   D. 散点图
2. 某考生在一项测验中得分60，经换算百分等级为70，这表明在所有考生中，得分低于该考生的人数占总人数的（ ）。（统考2007研）
   A. 30%
   B. 40%
   C. 60%
   D. 70%
3. 适用于描述某种心理属性在时间上变化趋势的统计分析图是（ ）。（统考2010研）
   A．茎叶图
   B．箱形图
   C．散点图
   D．线形图
4. 运用相对累加次数分布曲线，可以快速计算出与学生原始分数相对应的统计量是（ ）。（统考2010研）
   A．百分等级
   B．Z分数
   C．T分数
   D．频次
5. 下列常用统计图中，适合描述部分在总体中所占比例的图形是（ ）。（统考2015研）
   A. 箱形图
   B. 线形图
   C. 条形图
   D. 圆形图
6. 某考生得分为81，在下列次数分布表中，能够直接判断有多少考生得分比他低的是（ ）。（统考2013研）
   A. 简单次数分布表
   B. 分组次数分布表
   C. 累加次数分布表
   D. 相对次数分布表
7. 测验总分的分布呈负偏态，说明测验整体难度（ ）。（统考2008研）
   A. 偏难
   B. 偏易
   C. 适中
   D. 无法判断

第三章 集中量数

选择题

1. 一个呈负偏态分布的随机变量，其众数、中数、算术平均数的大小关系是（ ）。（统考2016研）
   A. 三者相等
   B. 众数最小
   C. 中数最小
   D. 算术平均数最小
2. 在一组在正态分布的数据中，两端各增加一个极值后，一定不会受到影响的统计特征值是（ ）。（统考2015研）
   A. 全距
   B. 众数
   C. 平均数
   D. 标准差
3. 有组数据：2，3，4，5，6，7，8。该组数据的平均数和标准差分别是5和2。如果给这组数据的每个数都加上3，再乘以2，那么可以得到一组新数据。其平均数和标准差分别是（ ）。（统考2013研）
   A. 8，2
   B. 8，5
   C. 16，4
   D. 16，10
4. 数据2、5、9、11、8、9、10、13、10、24中位数是（ ）。（统考2012研）
   A. 8.0
   B. 8.5
   C. 9.0
   D. 9.5
5. 一组数据的分布曲线呈双峰状态，据此可以推测该组数据中可能有两个（ ）。（统考2012研）
   A. 中数
   B. 众数
   C. 平均数
   D. 几何平均数
6. 有一组数据：3，6，2，7，32，4，8，6，5。要描述这组数据的特征，受极端数据值影响的统计量是（ ）。（统考2008研）)
   A. 平均数
   B. 中数
   C. 四分位数
   D.众数

简述题

1. 简述算术平均数的使用特点(浙大2003研 ,苏州大学2002研)
2. 算术平均数和几何平均数分别适用于什么情形?(南开大学2004研)

第四章 差异量数

选择题

1. 某学生在智力测验上的IQ为115,如果利用另外的方式报告分数,还可以表示为（ ）。（统考2016研）
   A. 标准分数1
   B. T分数60
   C. 百分等级84
   D. 标准分数8
2. 瑞文推理测验的常模分数采用的是（ ）。（统考2014研）
   A. 百分数
   B. 四分位差
   C. 百分位差
   D. 百分等级
3. 下列选项中,具有等距单位的常模参照分数是（ ）。（统考2014研）
   A. 发展顺序量表
   B. 教育商数
   C. T 分数
   D. 百分等级
4. 比较同一团体不同属性特质观测值的离散程度,恰当的统计指标是（ ）。（统考2014研）
   A. 全距
   B. 方差
   C. 四分位差
   D. 变异系数
5. 下列几组数据中，标准差最大的一个是（ ）。（统考2013研）
   A. -2, -1, 0, 1, 2
   B. 2, 6, 10, 14, 18
   C. 5.756, 5.765, 5.890, 5.923
   D. 1.00, 1.25, 1.50, 1.75, 2.00, 2.25, 2.50, 2.75, 3.00
6. 某测验用百分等级表示测验结果，其受测者的测验结果低于平均分的一个标准差。他在该组被试中的百分等级是（ ）。（统考2013研）
   A. 10
   B. 16
   C. 34
   D. 50
7. 小明在一次由50人参加的英语测验中得了80分，排名第8，其百分等级为（ ）。（统考2012研）
   A. 160
   B. 80
   C. 85
   D. 88
8. 一组数据的平均数是100，标准差是25，这组数据的变异系数是（ ）。（统考2008研）
   A. 4%
   B. 25%
   C. 4
   D. 25
9. 在某次考试中，小明的语文、数学成绩均为80，英语成绩为75。已知全班三科平均成绩都为65，语文标准差为10，数学标准差为15，英语标准差为5。小明三科的成绩按照标准分由大到小进行排序的结果是（ ）。（统考2008研）
   A. 语文、数学、英语
   B. 英语、数学、语文
   C. 英语、语文、数学
   D.语文、英语、数学
10. 一组服从正态分布的数据，平均数为50，标准差为5，则Z值为-2.58的原始数据是（ ）。（统考2008研）
    A. 37.10
    B. 42.42
    C.47.42
    D.62.90

概念题

1. 差异系数(浙大2003研)
2. 四份差(中科院2004研)
3. 集中量数与差异量数(浙大2000研,苏州大学2002研)
4. T分数(华中师大2004研)
5. 标准分数(华中师大2006研)

计算题

1. 计算未分组数据: 18,18,20,21,19,25,24,27,22,25,26的平均数, 中位数和标准差(首师大2003研)
2. 把下列分数转换成标准分数 11.0, 11.3, 10.0, 9.0, 11.5, 12.2, 13.1, 9.7, 10.5 (华南师大2003研)

第五章 相关关系

选择题

1. 下列哪个相关系数所反映的相关程度最大（ ）。
   A. r=0.53
   B. r=-0.69
   C. r=0.37
   D. r=0.72
2. 积差相关的提出者是英国统计学家（ ）。
   A. 斯皮尔曼
   B. 皮尔逊
   C. 高斯
   D.高尔顿
3. 计算积差相关需要满足（ ）。
   A. 要求是等级数据
   B. 两列变量各自总体的分布都是正态
   C. 两个相关变量都是连续变量
   D. 两个变量之间的关系应该是直线型的
4. 如果相互关联的两个变量，一个增大另一个也增大，一个减小另一个也减小，变化方向一致，这两个变量之间有（ ）。
   A. 零相关
   B. 正相关
   C. 负相关
   D. 完全相关
5. 当我们按性别差异，将男性指定用数字“1”来代表，女性指定用数字“2”来代表，这里所得到的数据是（ ）。
   A. 称名变量
   B. 顺序变量
   C. 等距变量
   D. 比率变量
6. 质量相关包括（ ）。
   A. 点二列相关
   B. 二列相关
   C. 多系列相关
   D. 积差相关
   E. 等级相关
7. 两个变量分布都是真正的二分变量，要计算两者之间的关系系数，最恰当的方法是（ ）。（统考2016研）
   A. 四分相关
   B. $\phi$相关
   C. 二列相关
   D. 点二列相关
8. 有300名考生，期中和期末成绩的相关系数为0.62，两次考试成绩平均分数均为80分，如给所有考生的期中成绩各加8分，加分后两次成绩的相关系数是（ ）。（统考2016研）
   A. 0.52
   B. 0.62
   C. 0.70
   D. 0.72
9. 当积差相关系数r=0时，对两个变量之间关系的最佳解释是（ ）。（统考2013研）
   A. 相关程度很低
   B. 不存在任何相关
   C. 不存在线性相关关系
   D. 存在非线性相关关系
10. 两列变量是等距或等比变量，且服从正态分布，计算相关系数最恰当的方法是（ ）。（统考2012研）
    A. 积差相关
    B. 等级相关
    C. 点二列相关
    D. 双列相关
11. 一个测验由0、1计分的100道单选题构成.根据原始得分计算题目分度的恰当方法是（ ）。（统考2017研）
    A. Φ相关 　　
    B. 点二列相关　
    C. 等级相关　
    D. 四分相关
12. 一项研究调查了不同性别的成年人对在公众场合吸烟的态度，结果如表所示。那么，性别与对待吸烟的态度之间的相关系数是（ ）。（统考2008研）
    A. 0.12
    B.0.32
    C.0.48
    D.0.54
13. 对于具有线性关系的两列正态分布的连续变量，计算它们相关系数最恰当的公式是是（ ）。（统考2008研）
    A. r=1-6ξD2/N/(N2-1)
    B. r=Xp-Xq/Spq
    C. r=Xp-Xq/Stpq/y
    D. r=ξxy/NSxSy

概念题

1. 相关系数（吉林大学2002研）
2. 二列相关（中科院2004研）

简答题

1. 简述使用积差相关系数的条件（首师大2004研）
2. 哪些测量和统计的原因会导致两个变量之间的相关程度被低估（北师大2004研）
3. 如果你不知道两个变量概念之间的关系，只知道从两个变量的相关系数很高，请问你可能做出什么样的解释？（武汉大学2004研）
4. 一个变量的两个水平间的相关很高，是否说明两水平的均数间没有差异呢？为什么？举例说明。（中山大学2004研）
5. 简述正态分布与标准正态分布的区别与联系。（统考2008研）

计算题

1. 4名教师各自评阅相同的5篇作文，表2为每位教师给每篇作文的等级，试计算肯德尔W系数（首师大2003研）
   教师对学生作文的评分

   作文		评分者
   	1	2	3	4
   一	3	3	3	3
   二	5	5	4	5
   三	2	2	1	1
   四	4	4	5	4
   五	1	1	2	2

2. 五位教师对甲乙丙三篇作文分别排定名次如下表
   

   名次		教师序号
   	甲	乙	丙
   1	3	1	2
   2	3	2	1
   3	3	1	2
   4	1	3	2
   5	1	3	2

   
   请对上述数据进行相应的统计分析。（华东师大2003研）

第六章 概率分布

单选题

1. 总体服从正态分布且方差已知时，其样本平均数的分布是（ ）。（统考2010研）
   A. 卡方分布
   B. t分布
   C. F分布
   D. 正态分布
2. 简单随机抽样方法抽取样本,如果要使得抽样标 准误降低50%,则样本容量需扩大的倍数为（ ）。
   A. 2
   B. 4
   C. 5
   D. 8
3. 关于t分布与标准正态分布两者之间的关系,正确 的表述是（ ）。
   A. T分布的均值大于标准正态分布的均值。
   B. 标准正态分布的标准差大于t分布的标准差。
   C. 两者的标准差、均值都相同。
   D. 随着自由度增大,t分布接近于标准正态分布。
4. 有10道是非题，要从统计上(99%的把握)判断一个被试是否因猜测因素答对，他至少应正确回答的题目数是（ ）。（统考2013研）
   A. 5
   B. 6
   C. 7
   D. 8
5. 美国教育考试服务中心采用△=13+4Z表述题目难度，式中△字母表示题目难度值，Z表示由P值转换得来的标准分数，其取值范围为-3—3。根据正态分布表，下列表述错误的是（ ）。（统考2016研）
   A. △属于等比量尺
   B. △值越大，题目越难
   C. 通过率P=0.50时，△=13
   D. △以25为上限，1为下限
6. 下列有关正态曲线模型,不正确的是（ ）。（统考2014研）
   A. 曲线以平均数为对称轴
   B. y值越大,P值越大
   C. 曲线与 轴之间区域面积为1
   D. 曲线呈现”中间高,两边低”的形状
7. 两个骰子掷一次,出现两个相同点数的概率是（ ）。（统考2014研）
   A. 1/3
   B. 1/6
   C. 1/12
   D. 1/36
8. 样本平均数抽样分布趋向正态分布的必要条件是（ ）。（统考2015研）
   A. 总体分布单峰,对称
   B. 总体均值,方差已知
   C. 总体分布不限,大样本
   D. 总体分布正态,样本方差已知
9. 在下列导出分数中，不具等距性的是（ ）。（统考2013研）
   A. 百分等级
   B. 2分数
   C. T分数
   D. CEEB次数
10. 下列统计分布中，不受样本容量变化影响的是（ ）。（统考2013研）
    A. 正态分布
    B. t分布
    C. $\chi^2$分布
    D. 二项分布
11. 下列关于效果量的表述，错误的是（ ）。（统考2013研）
    A. 效果量是H，不为真的程度
    B. 效果量提供了差异大小的信息
    C. 效果量是实验处理的效应大小
    D. 效果量反映自变量与因变量关系的程度
12. 能够反映估计量精确性的统计量是（ ）。（统考2013研）
    A. 标准误
    B. 标准差
    C. 方差
    D. 四分位差
13. 比较不同心理特质的两组数据的离散程度时，应采用的统计量是（ ）。（统考2017研）
    A. 差异系数
    B. 四分位差
    C. 平均差
    D. 标准差
14. 某被试的书氏智力测试分数比同年龄常模团体的均值高一个标准差，其IQ是（ ）。（统考2017研）
    A. 120　　
    B. 115　
    C. 110
    D. 105
15. 下列导出分数中，不属于等距变量的是（ ）。（统考2017研）　　
    A. 百分等级
    B. CFEB 分数
    C. Z 分数
    D. T 分数

多选题

1. 影响统计功效的因素有（ ）。（统考2016研）
   A. 处理效应大小
   B. 显著性水平的设定
   C. 检验的方向性
   D. 样本容量
2. 在心理学科学的调查研究中,通常不可避免的误差有（ ）。（统考2016研）
   A. 系统误差
   B. 随机误差
   C. 组间误差
   D. 抽样误差

概念题

1. 古典概率（中科院2004研）
2. 抽样分布（中科院2005研）

简答题

1. 二项试验应满足哪些条件？（中科院2004研）
2. 正态分布的特征是什么，统计检验中为什么经常将正态分布转化成标准正态分布?（北师大2003研，上海师大2002研）
3. 正态分布的标准差有何统计意义，在统计检验中为什么会用到标准差？（北师大2003研）
4. 简述正态分布与标准正态分布的区别和联系（统考2008研）

第七章 参数估计

单选题

1. 一次测验的分数的服从方差为25的正态分布，某学校共有100名学生参加测试，其平均值为70分，若置信水平为0.99，则总体平均值的置信区间为（ ）。（统考2010研）
   A. [69.5 70.57]
   B. [68.71 71.29]
   C. [67.52 72.48]
   D. [63.55 76.45]
2. 当样本容量一定时，置位区间的宽度（ ）。（统考2013研）　　
   A. 随着显著性水平α的增大而增大
   B. 随着显著性水平α增大而减小
   C. 与显著性水平α无关
   D. 与显著性水平α的平方根成正比
3. 抽取一个容量为50的样本，其均值为10，标准差为5，其总体均值95%的置信区间为（ ）。（统考2017研）
   A. [8.60 ,11.40]
   B. [8.04 ,11.96]
   C. [7.65 ,12.35]
   D. [6.90 ,13.10]

概念题

1. 无偏估计（中科院2004研）
2. 标准误差（中科院2005研，南开大学2006研）

简答题

1. 简述点估计和区间估计 （首师大2003研）
2. 在心理学研究中，以样本对总体判断的数理理论依据（首师大2003研）
3. 为什么要做区间估计？怎样对平均数做区间估计？（北师大2003研）

计算题

1. 在学校的一次考试中，已知全体学生的成绩服从正态分布，其总方差为100。从中抽取25名学生，其平均成绩为80，方差为64。以99%的置信度估计该学校全体学生成绩均值的置信区间是？（统考2003研）

第八章 假设检验

选择题

1. 单尾Z检验中,α确定为0.01时,其统计决策的临界值为（ ）。（统考2014研）
   A. 1.64
   B. 1.96
   C. 2.33
   D. 2.58
2. 研究人员要检验20对分开抚养的同卵双生子在15岁时智力测验分数的差异，最恰当的检验方法是（ ）。（统考2013研）
   A. 两相关样本的t检验
   B. 两独立样本的t检验
   C. 样本与总体均数的t检验
   D. $\chi^2$检验
3. 随机抽取一个样本容量为100的样本，其均值 平均值=80，标准差S=10，所属总体均值u的95%的置信区间为（ ）。（统考2012研）
   A. [78.04，81.96]
   B. [60.40，99.60]
   C. [76.08，83.92]
   D. [79.80，80.20]
   根据材料答以下三题
   已知X1、X2为两个相互独立的连续变量，两个总体均为正态分布，X1, X2, n1=11, n2=10, s1=144, s2=121。检验平均数是否存在显著差异。（统考2012研）
4. 在进行假设检验之前，需要（ ）
   A. 检验两个样本的联合方差是否齐性
   B. 检验两个样本的方差是否齐性
   C. 检验两个总体的方差是否齐性
   D. 用样本方差估计总体方差
5. 对这两个变量的均值进行差异检验，最恰当的方法是（ ）
   A. t检验
   B. Z检验
   C. q检验
   D. $\chi^2$检验
6. 差异检验的自由度为（ ）
   A. 9
   B. 10
   C. 19
   D. 20
7. 研究者筛取了 28 对夫妻.考查双方承受压力的差异，正确的验证方法是（ ）。（统考2017研）
   A. 独立 t 检验，双侧假设检验
   B. 配对 t 检验，单侧假设检验
   C. 配对 t 检验，双侧假设检验
   D. 独立 t 检脸，单侧假设检验
8. 统计功效是（ ）。（统考2017研）
   A. $\alpha$
   B. $\beta$
   C. 1- $\alpha$
   D. 1- $\beta$
9. 在假设检验中，通常用来表示统计检验力(power of test)的是（ ）。（统考2008研）
   A. $\alpha$
   B. 1-$\beta$
   C. $\alpha$+$\beta$
   D. $\alpha$-$\beta$

概念题

1. 统计检验力（浙大2000研）
2. 检验的显著性水平 （南开2004研）

简答题

1. 简述统计假设检验中两类错误的定义及其关系（统考2009研）
2. 在进行差异的显著性检验时，若将相关样本误做独立样本处理，对差异的显著性有何影响，为什么？（北师大2003研）
3. 有人说“t检验适用于样本容量小于30的情况，Z检验适用于大样本检验”，谈谈你对此的看法（北师大2004研）
4. 选择统计检验程序的方法时需要考虑哪些条件，才能正确应用统计检验方法分析问题（北师大2004研）
5. 独立样本和相关样本之间的差别（中山大学2004研）
6. 简述t检验和方差分析方法在进行组间比较上的区别和联系。

计算题

1. 随机从某总体选取10名被试，分别实施两次数学测验，两次测验的成绩见下表，问被试在两次测验的平均数是否有显著差异？试对结果进行解释（α=0.05，df=9，t=2.262；df=18，t=2.552）（首师大2003研，浙大2008研）
   表 10名被试两次测验的成绩

   被试	1	2	3	4	5	6	7	8	9	10
   测验1	65	48	63	52	61	53	63	70	65	66
   测验2	61	42	66	52	47	58	65	62	64	69

第九章 方差分析

单选题

1. 与Fisher方法相比，Tukey氏HSD方法检验（ ）。
   （1）更保守
   （2）具有更大的检验力
   （3）更不易控制$\alpha_{EW}=0.05$的增大
   （4）使用更小的临界值
2. 某研究中共有3组被试，每组12人，进行方差分析时，误差自由度为（ ）。（统考2016研）
   A. 2
   B. 11
   C. 33
   D. 35
3. 在探讨性别与被试年龄(青年、中年、老年)对某品牌手机偏好影响的研究中,其实验设计为（ ）。（统考2014研）
   A. 2×3 设计
   B. 1×3 设计
   C. 2×2 设计
   D. 3×3 设计
4. 应用方差分析检验一元线性回归方程的有效性，其回归自由度和残差度分别为（ ）。（统考2012研）
   A. 1和n-1
   B. 1, n-2
   C. 2, n-1
   D. 2, n-2
   根据下表所示的实验设计方案，回答以下三题。 （统考2012研）
   4种实验处理的实验设计

   被试		实验处理
   A	1	2	3	4
   B	2	3	1	4
   C	3	4	4	1
   D	4	1	3	2

5. 这种设计属于（ ）
   A. 被试间设计
   B. 混合设计
   C. ABBA设计
   D. 被试内设计
6. 采用这种设计可控制的主要额外变量是（ ）
   A. 顺序误差
   B. 期望误差
   C. 实验者效应
   D. 动作误差
7. 如果有6种实验处理，采用这种设计的被试人数可以是（ ）
   A. 8人
   B. 10人
   C. 12人
   D. 14人
8. 一个实验有三组被试，各组被试人数相同，方差分析的总自由度为29，该实验的被试数为（ ）。（统考2017研）
   A. 8
   B. 9
   C. 10
   D.11
9. 在一个3×3的实验设计中，存在的交互作用有（ ）。（统考2008研）
   A. 1个
   B. 3个
   C. 6个
   D. 9个
10. 方差分析需要满足的前提条件有（ ）。（统考2008研）
    A. 总体正态分布
    B. 各处理方差齐性
    C. 总体方差已知
    D. 各组样本容量相同

多选题

1. 重复测量设计方差分析的假设有（ ）。（统考2015研）
   A. 不同处理水平下的总体方差相等
   B. 每个处理条件内的观察都是独立的
   C. 不同处理水平下的总体服从正态分布
   D. 因变量的方差-协方差矩阵符合球形假设
2. 下列关于$\chi^2$检验与方差的分析的表述，正确的有（ ）。（统考2013研）
   A. 两者都是无方向性的检验方法
   B. $\chi^2$检验的方差分析都必须做齐性检验
   C. $\chi^2$检验属非参数检验，方差分析属参数检验
   D. $\chi^2$检验与方差分析都要求测量数据呈正态分布
3. 对一个2x3被试内设计实验结果进行统计分析，能得到的信息有（ ）。（统考2017研）
   A．主效应
   B．简单主效应
   C．被试阅读误差
   D．交互作用

简答题

1. 方差分析的适用条件是什么？主要用来检验什么？（东北师大2006研）

计算题

1. 以下实验中，各有多少对互不相同的成对比较：
   （1）实验中有5个组？
   （2）实验中有8个组？
   （3）实验中有10个组？
2. 在下列实验中，student化全距统计量(q)的临界值是多少？（α_EW =0.05）
   （1）4个组，每个组6个参加者
   （2）6个组，每个组4个参加者
   （1）8个组，每个组16个参加者
3. 一名研究者正在研究日常锻炼和吃素对静息心率的影响。两个因素（锻炼的人vs.不锻炼的人，素食者vs. 非素食者）交互生成了一个2x2的矩阵，每个单元里有10人。每个单元的均数（m）和无偏标准差（s）如下:
   

   	锻炼	不锻炼
   素食	m=60	m=70
   	s=15	s=18
   非素食	m=65	m=75
   	s=16	s=19

   
   (1) $MS_w$是多少？
   (2) 计算三个F值（提示：检查是否存在交互作用。如果不存在，计算会简单些），并提出你的结论。
   (3)如果每个单元有40人，这些F值会有多大？将这些值与（2）的结果比较。样本量的增加对F有什么影响？（精确的数学表达式是什么？）
   (4)从（3）得到的F值你可以下什么样的结论？这些结论的局限性是什么（在因果方面）？
4. 有四种数学实验教材，为比较其教学效果，按随机化区组设计将学校分为三个区组，在每个区组中随机抽取4所学校，它们分别被随机地指定一种实验教材授课。经一年教学后通过统一考试得到每所学校的平均成绩。请完成下列方差分析表，并检验四种教材的教学效果是否有显著差异？（中科院2006研）

   变异来源	平方和	自由度	均方	F	F0.05
   					4.76
   区组	42.12				5.14
   误差	67.38
   总变异	1993.06

5. 研究者欲研究某城市居民环境保护的动机类型(A因素：短暂类型，长远动机)和环保行为(B因素：宣传、批评、治理)对所在社区环境的影响，研究者采用组间设计，每种处理方式下研究了10位成年居民。下面尚未填写完毕的研究结果的方差分析表，请给出方差分析表中括号内对应的数值。 （统考2013研）

   变异来源	SS	df	MS	F
   组间
   A	280	1	280	（）
   B	48	2	24
   AxB	120	（）	60
   组内	540	（）	（）
   总和	（）

6. 根据方差分析表回答问题
   

   变异来源	SS	df	MS	F
   A因素	6	2	3
   B因素	12	1	12
   AxB	26
   残差	192	66	2.91
   总和	236	71

   
   （1）计算AxB 的自由度、均方。
   （2）检验B以及AxB的显著性。

综合题

1. 在一项眼动研究中，呈现不同特征的人脸图片（正面、侧面、斜视、直视），来考察被试对这些图片的考察特点，每种实验条件单独为一个实验单元，每一实验单元包含64个试次，每个被试共完成256个试次。实验结果如下图所示，方差分析表明，各因素的主效应显著，其中一个因素的方差分析结果为F(1,15)=20.598，p<0.001；因素之间的交互作用显著。清回答下列问题。（统考2016研）
   （1）该研究为何种实验设计？说明这种实验设计的特点。
   （2）指出该研究中的因素和水平，以及使用的被试数量。
   （3）根据方差分析结果和下图，说明所能得到的实验结论。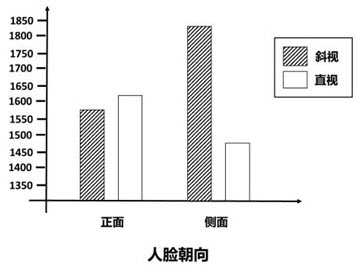
   
2. 表1和表2、表3和表4是针对同一问题采用两种不同的实验设计所获得的模拟实验研究结果。请据此回答下列问题： （统考2008研）
   实验设计一：
   （暂缺）表一：不同教学方法下不同类型学生的学习习惯
   表二：方差分析结果
   

   变异源	平方和	自由度	均方	F值	P值
   教学方法	1040.17	1	1040.17	11.92	0.003
   学生类型	322.67	1	322.67	3.698	0.068
   教学方法*学生类型	580.17	1	580.17	6.649	0.018
   误差	1745	20
   总和	3688	23

   
   实验设计二
   表三：不同教学方法下不同类型学生的学习成绩
   

   		教学方法
   		讲授式	启发式	平均分
   学生类型	学优生	48.17	51.5	49.83
   	学困生	45.67	68.67	57.17
   平均分		46.92	60.08	53.5

   
   表四：方差分析结果
   

   变异源	平方和	自由度	均方	F值	P值
   被试间效应
   学生类型	322.67	1	322.67	0.442	0.151
   误差（学生类型）	1322.33	10	132.23
   被试内效应
   教学方法	1040.17	1	1040.17	25.206	0.001
   教学方法*学生类型	580.17	1	580.17	14.059	0.004
   误差	412.67	10	41.27

   
   （1）分别指出这两种实验各自属于何种设计类型，每种设计各自使用了多少被试。
   （2）针对研究问题，根据实验设计一的统计分析结果，能得出什么结论？实验设计二与实验设计一的结论是否相同？如果不同，能得出什么结论？ （3）这两种设计中哪一种更适宜考察本研究的问题？请具体说明理由。

第十章 卡方检验

单选题

1. 能够处理某一行为出现的理论次数与实际次数之间差异的统计检验方法是（ ）。（统考2010研）
   A. t检验
   B. Z检验
   C. $\chi^2$检验
   D. F检验
2. 某研究将工人、农民、公务员、上任安生活满意度分为满意、不满意、介于两者之间，观察研究不同职业人员之间的生活满意度差异，分析该研究数据最恰当的统计方法是（ ）。（统考2012研）
   A. 相关分析
   B. $\chi^2$检验
   C. 因素分析
   D. t检验

多选题

1. 下列关于χ2分布的特点描述，正确的有（ ）。（统考2012研）
   A. $\chi^2$取值均为正值
   B. $\chi^2$分布是正偏态分布
   C. $\chi^2$分布为非连续性分布
   D. $\chi^2$分布的标准差与自由度相同

简答题

1. 判断某个变量X的样本是否符合卡方分布的方法是什么？（中山大学2004研）
2. T检验，F检验，卡方各自适用于什么情况？（北师大2003研）

计算题

1. 一研究者随机调查了8名看过A和B两部电影的受访者，问他们更喜欢哪部电影。6名受访者喜欢电影A，2名受访者喜欢电影B。他就此得出结论：电影A更受观众所喜欢。但实际上也有可能这两部电影为观众同等程度所喜欢而使得这个结论是错误的，发生这种错误的概率是多少？（计算结果用分数表示）（南开2004研）
2. 5名接受预防注射的实验组中，2名在规定时间患感冒，而在15名的控制组中，却有9名患感冒。问：预防注射是否有用？（首师大2004研）
3. 近一个世纪以来,某城市的居民患抑郁、焦虑症和强迫的比例非常接近.近期,心理学家为了考察该城市居民的心理健康状况,进行了一次调查,表明,抑郁患者85人,焦虑患者124人,强迫患者91人.请问该城市居民的三种神经症患者比例是否发生显著变化? ($\chi_{0.05}^2(2)=5.99$,$F_{0.05}(3.2)=9.55$,$Z_{0.05}=1.96$)。（统考2016研）

第十一章 非参数检验

多选题
下列关于非参数检验的表述，正确的有（ ）。（统考2017研）
A．适用于小样本　　　　　　　
B．变量总体须服从二项分布
C．适用于顺序数据资料　　　　
Ｄ．未能充分利用资料的全部信息

概念题

1. 非参数检验（华东师大，西北师大，苏州大学2002研）

简答题

1. 简述非参数检验的意义和常用方法。（浙大2003研）
2. 面对同一批数据，非参数方法和参数方法都适用，请问你会选择哪种方法？为什么？（武汉大学2004研）
3. 有14名智力水平相近的被试随机分配在三种不同的时间倒计时情境（主考提醒、挂钟提醒、自我提醒）下参加某一智力竞赛。（统考2010研）。 下表为三种时间倒计时提醒情境下被试回答正确的竞赛题数，经检验方差齐性。
   表1 三种时间倒计时提醒情境下被试智力竞赛结果
   

   主考提醒	挂钟提醒	自我提醒
   7	10	6
   7	9	8
   5	8	7
   10	8	8
   	10	9

   
   请回答下列问题：
   （1）参数检验的方差分析与非参数检验的方差分析有何异同。
   （2）选择一种恰当的参数检验方法进行参数检验，或使用克－瓦氏单因素方差分析进行非参数检验，并对统计检验结果做出解释。

第十二章 线性回归

单选题

1. 在回归方程中，其他条件不变，X与Y相关系数趋于0时，估计的标准误将会（ ）。（统考2010研）
   A. 不变
   B. 提高
   C. 降低
   D. 趋近于0
2. 一元线性回归方程，有效性检验及解释率的计算方法是（ ）。（统考2016研）
   A. 偏相关分析和计算信度系数
   B. 方差分析和计算决定系数
   C. 多重检验和计算回归系数
   D. 因素分析和计算拟合指数
3. 研究人员建立了线性回归方程。现有一个样本的自变量分别是3、4、3、4、6，可预测因变量的平均数为（ ）。（统考2015研）
   A. 1.75
   B. 2.00
   C. 13.00
   D. 17.00
4. 在回归分析中，考察回归效果使用的指标是（ ）。（统考2008研）
   A. 内部一致性系数
   B. 决定系数
   C.概化系数
   D.列联系数

多选题

1. 线性回归分析的前提假设有（ ）。（统考2011研）
   A. 变量总体服从正态分布
   B. 个体间随机误差相互独立
   C. 自变量的个数多于因变量的个数
   D. 因变量与自变量存在线性关系

简答题

1. 如何确认变量之间有因果关系？回归方程中自变量X和因变量Y是否肯定有因果关系？（北师大2006研）
2. 简述最小二乘法。（中科院2004研）
3. 毕业考试成绩为x，智力测验分数为y，已知这两者的r_xy=0.5，IQ=100+15x，某学校根据学业考试成绩录取学生，录取率为15%，若一个智商为115的学生问你他被录取的可能性为多少,你如何回答他 （北师大2004研）
4. 为什么要建立回归方程? （中山大学2004研）
5. 最小二乘法中各点到拟合直线的距离为什么要取铅直距离而不取垂直距离？（武汉大学2004研）
6. 有一数列t₁,t₂,…,t_n, 令$Y=\sum_{i=1}^n (t_i-K)^2$。K为何值时Y最小？证明你的结论（南开大学2004研）
7. 现有一项关于学生学习的动机水平与学习成绩的关系的研究,在分析两者的关系时,有人建议用相关分析,有人建议用回归分析。 （统考2014研）
   (1)简述相关分析和回归分析的区别和联系。
   (2)若学生动机水平与学习成绩的相关系数为0.95, 能否判断学习成绩的变异可用动机水平来解释? 如果可以,解释量是多少?如果不可以,为什么?
   (3)已知动机水平的平均数为38.6,标准差为21.6,学习成绩平均数为33.8,标准差为 18.76,求回归方程。

计算题

1. 150名6岁男童体重（x）与曲臂悬体（y）的相关系数r=0.35，$\bar x$=20公斤，$\sigma_x$=2.55, $\bar y$=42.7秒，$\sigma_x$=8.2, 试估计体重22.6公斤的男童，曲臂悬体为多少秒？（首都师大2004研）
2. 下表给出了某班12名同学两次考试的成绩。要求：
   （1） 计算两次考试成绩的相关
   （2） 求y对x的线性回归方程
   （3） 对所求方程进行方差分析，以检验其显著性（浙大2003研）

   被试	1	2	3	4	5	6	7	8	9	10	11	12
   考试一(X)	65	63	67	64	68	62	70	66	68	67	69	71
   考试二(Y)	68	66	68	65	69	66	68	65	71	67	68	70

第十三章 多变量统计分析简介

选择题

1. 通常主要成分分析要求所选择的主成分对应的特征根λ应该是（ ）。（统考2014研）
   A. $\lambda<0$
   B. $\lambda=0$
   C. $0<\lambda<1$
   D. $\lambda\geq 1$
2. 心理学研究中,协方差分析能够（ ）。（统考2014研）
   A. 控制无关变异
   B. 使实验变异最大化
   C. 减少个体误差
   D. 减少随机误差

概念题

1. 逐步回归（浙大2000研）
2. 嵌套设计 （华中师大2004研）
3. 协方差分析 （华东师大2002研）

简答题

1. 什么是二元线性标准回归方程？（华东师大2003研）

2. 在一项社会心理学研究中，研究者给男性试看详细的案件资料，让他们摄像自己是法官，对罪犯进行判决。所有罪犯都是女性。实验将被分为两组：一组被试阅读的素件材料附有漂亮的罪犯照片（有魅力组）；一组被试阅读的案件材料附有缺乏吸弓｝力的罪犯照片（无魅力组）。案件材料涉及两种犯罪类型，一种是诈骗罪，一种是偷盗罪，实验结果见下表。（统考2017研）
   判刑的平均年数
   

   	照片类型
   案件类型	有魅力	无魅力
   诈骗	5.45	4.35
   偷盗	2.8	5.2

   
   （1）简要说明该实验设计的类型。
   （2）用线性图描述结果，并作简要分析。

第十四章 抽样原理及方法

单选题

1. 关于分层随机抽样的特点，表述正确的是（ ）。（统考2011研）
   A. 总体中的个体被试抽取的概率相同
   B. 所有被试在一个层内抽取
   C. 层间异质，层内同质
   D. 层间变异小于层内变异
2. 当样本容量增大一倍时，总体平均数的置信区间长度会（ ）。（统考2016研）
   A. 扩大一倍
   B. 缩小一倍
   C. 扩大1.414倍
   D. 缩小1.414倍
3. 当总体中的个体具有周期性规律是，不适用抽样方法是（ ）。（统考2015研）
   A. 简单随机抽样
   B. 分层抽样
   C. 等距抽样
   D. 方便抽样
4. 用简单随机抽样方法抽取样本，如果要使抽样标准误降低50%，则样本容量需扩大倍数为（ ）。（统考2012研）
   A. 2
   B. 4
   C. 5
   D. 8
5. 某企业考察不同工龄员工的离职意向，将整个企业3000名员工按工龄分为三组，两年以下有1000人，两年至五年有1500人，五年以上有500人。如果采用按比侧分层随机抽样的方法取容量为600的样本，那么，从两年至五年工龄的员工中应抽取的人数为（ ）。（统考2017研）
   A. 100
   B. 200
   C. 300
   D. 400

概念题

1. 分层随机抽样（浙大2003研）
2. 抽样误差 （中科院2004研）
3. 随机原则 （华南师大2003研）

简答题

1. 2002年10月29日，《江南日报》发布中华英才网的调查报告，调查结果显示南京职工的人均月薪已达2690元，有人认为这一结果高估了南京人的月收入。你怎么看这个结果，试分析高估的原因。（北师大2003研）
2. 如果两总体中的所有个体都进行了智力测验，这两个总体智商的平均数差异是否还需要统计检验？为什么？（北师大2004研）
3. 某厂要进行压力的性别差异研究，但由于工厂不大就把男女员工的数据都收集起来了，那么应该用什么方法看性别间有否差异呢？（中山大学2004研）
4. 为了了解某校三年级480名学生的学习成绩，首先将他们的成绩分为上、中、下三层，各层人数分别为120、300、60，各层的标准差估计为10、12、13，假如要求从全年级中抽取60人，请用最优配置法计算各层应抽取的人数。（华东师大2003研）

本网站的部分内容如若涉及侵权问题，请速与作者联系。