第四章 差异量数
如何用少量数字来概括数据?
数据的‘位置’
均值,中位数,k百分位数,众数。
数据的“尺度”
论语有一句话:“不患寡而患不均”,这是指不怕财富少,而怕分配不公平而造成贫富差距太大。
贫富、多寡是由位置统计量来描述的,而是否“均”是由尺度统计量(scale statistic)来描述的。尺度统计量是描述数据散布,即描述集中与分散程度或变化(spread或variablity)的度量,因此,有人不无道理地建议用“散度统计量”这个名词。统计中有许多尺度统计量。
一般来说,数据越分散,尺度统计量的值越大。
为了说明,回顾第二章图2:中国、日本和美国的年龄的盒形图,可用看出来,从中位数来说,日本年龄较大,美国次之,中国最小,分布为69,66和49,而均值分布为69.1,65.5和52,但是这三个数据散布范围和模式很不一样。
最简单的尺度统计量就是极差(range),顾名思义,极差就是极大值和极小值之间的差。第二章例1数据的中日美三国富豪年龄的极差分布为41,52,和69岁,对应的图2种每个盒形图盒子的长度为上下两个四分位数之差,称为四分位极差或四分位间距(interquantile range),它描述了中间半数观测值的散步情况。
极差和四分位极差实际上各自只依赖于两个值,信息量太少。第二章例1数据的中日美三国富豪年龄的四分位极差分别为11.5,16.5和19.
另一个常用的尺度统计量为(样本)标准差(standard deviation)。它度量样本中各个数值到均值的距离的一种平均。标准差实际上是方差(variance)的平方根。样本方差是由各个观测值的均值距离的平方和除以减去1的样本量。
如果记样本中的观测值为x1,…,xn,则样本方差为
$$
s^2=\frac{1}{n-1}\sum_{i=1}^n(x_i-\bar{x})
$$
而样本标准差为样本方差的平方根,即s。
标准差由于和原始数据量纲一样,因此在数据分析中比方差用得更普遍。
显然,如果标准差越大,数据中的观测值就越分散,而小的标准差意味着数据很集中。
关于中日美三国富豪的标准差分别是8.4,15.1和13。
即使出于同一个总体,样本量相同的不同样本也会有不同的均值,这种来自许多不同样本的均值的标准差称为标准误差(standard error),也叫做均值的标准误差(standard error of mean)。
数据的标准得分
例3 (数据:grade.txt)该数据给出两个班(1班和2班)的同一门课程的成绩。假定两个班级水平类似,但是由于两个任课老师的评分标准不同,使得两个班成绩的均值和标准差都不一样。1班分数的均值和标准差分布为78.53和9.43,而二班的均值和标准差分别为70.19和7.00.那么得到90分的1班的A同学是不是比得到82分的2班的B同学成绩更好呢?怎么比较才能合理呢?
虽然这种均值和标准差不同的数据不能够直接比较,但是可以把它们进行标准化,然后再比较标准化后的数据。
一个标准化的方法是把某样本原始观测值(亦称得分,score)和该样本均值之差除以该样本的标准差,得到的度量称为标准得分(standard score,又称为z-score). 即,某观测值$x_i$的标准得分$z_i$定义为
$$
z_i=\frac{x_i-\bar{x}}{s}
$$
把各个样本的观测值都换成相应的标准得分,就可以进行比较了。
在本例中,
A的标准分为(90-78.53)/9.43=1.22
B的标准分为(82-70.19)/7=1.69
显然,如果两个班级水平差不多,B的成绩应该优于A的成绩,这是在标准化之前的数据中不容易看到的。
下图展示了着两个班级的原始成绩的盒形图(左边)和标准化之后成绩的标准得分的盒形图(右边)。可以看出,原始数据是在各自的中心值附近,而散布也不一样。但它们的标准得分则在0周围散布,而且散步也差不多。
实际上,任何样本经过这样的标准化后,就都变成均值为0、方差为1的样本。
标准化后不同样本观测值的比较只有相对意义,没有绝对意义。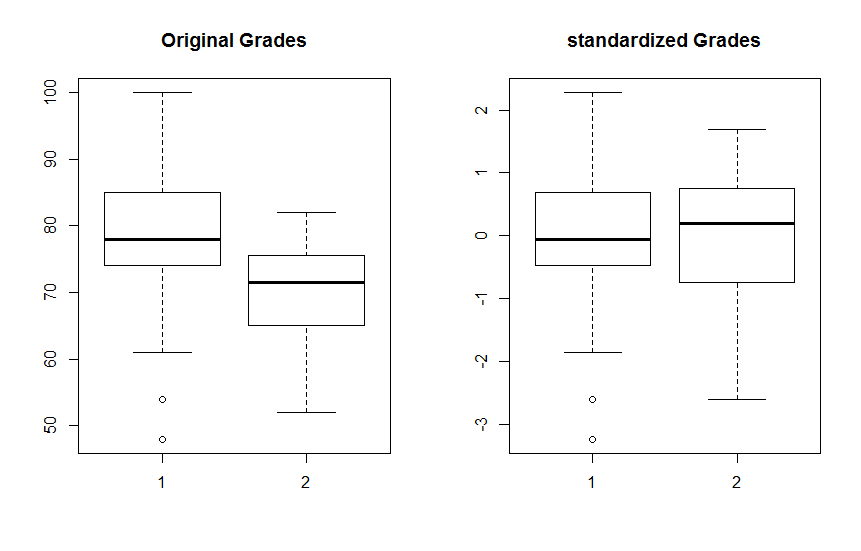
绘图的R代码为
|
|
标准化后的数据虽然总的尺度和位置都变了,但是数据内部点的相对位置没有变化。
计算标准得分仅仅是许多标准化方法中最常见的一种。
极差,四分位极差,标准差,方差,标准得分的R代码如下:
|
|