专题: Mixed-design analysis of variance
假设实验设计了两个因素(自变量):
- 当两因素均为Between-subject factors时,用Two-way ANOVA
- 当两因素均为Within-subject factors时,用Two-way repeated-measures ANOVA
- 当一个因素是Between-subject factor,另一个因素是Within-subject factor时,用 mixed-design ANOVA
一个混合设计方差分析的实验设计案例
2个因素:
- Within-subject factor = Time (4);
- Between-subject factor = Treatments (Group 1 & 2)
具体数据如下:
| Subject | Group | Time1 | Time2 | Time3 | Time4 |
| 1 | 1 | 3 | 4 | 7 | 3 |
| 2 | 1 | 6 | 8 | 12 | 9 |
| 3 | 1 | 7 | 13 | 11 | 11 |
| 4 | 1 | 0 | 3 | 6 | 6 |
| 5 | 2 | 5 | 6 | 11 | 7 |
| 6 | 2 | 10 | 12 | 18 | 15 |
| 7 | 2 | 10 | 15 | 15 | 14 |
| 8 | 2 | 5 | 7 | 11 | 9 |
Mixed-design ANOVA 的计算公式 Wikipedia
| Source | SS | df | MS | F |
| Between-subjects | ||||
| FactorBS | SSBS | dfBS | MSBS | FSBS |
| Error | SSBS/E | dfBS/E | MSBS/E | |
| Within-subjects | ||||
| FactorWS | SSWS | dfWS | MSWS | FWS |
| FactorWSxBS | SSBSxWS | dfBSxWS | MSBSxWS | FBSxWS |
| Error | FactorWS/E | dfWS/E | MSWS/S | Total | SST | dfT |
其中
$F_{BS} = \frac{MS_{BS}}{MS_{BS/E}}$,
$F_{WS} = \frac{MS_{WS}}{MS_{WS/S}}$,
$F_{BS\times WS} = \frac{MS_{BS \times WS}}{MS_{WS/E}}$.
相应的自由度计算如下:
dfBS = R – 1
dfBS(Error)= Nk – R
dfWS = C – 1
dfBSxWS = (R – 1)(C – 1)
dfWS(Error) = (Nk – R)(C – 1)
其中R为Between-subject的水平数,Nk为被试数,C为Within-subject的测试次数。因此,以上例子中,R=2,Nk=8,C=4。则:
dfBS = R – 1=2-1=1
dfBS(Error)= Nk – R = 8-2=6
dfWS = C – 1 =4-1=3
dfBSxWS = (R – 1)(C – 1)=(2-1)(4-1)=3
dfWS(Error) = (Nk – R)(C – 1)=(8-2)(4-1)=18
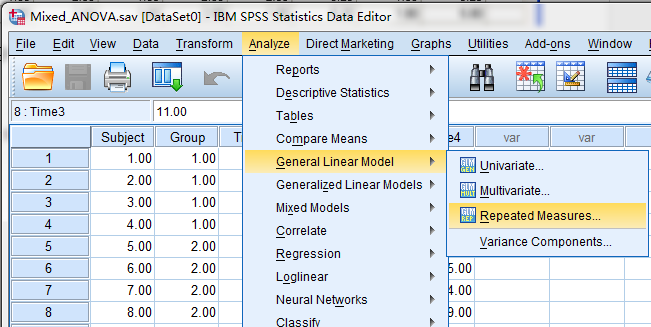
在SPSS中的运行Mixed-measuredANOVA的步骤如下:
打开对话框:Analyze - General Linear Model - Repeated Measures
定义Within-subject factor (name & level)
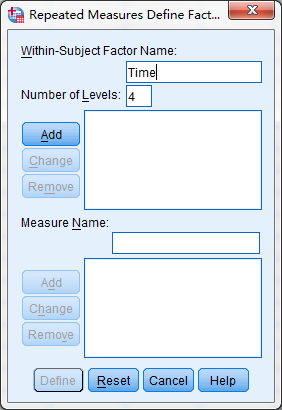
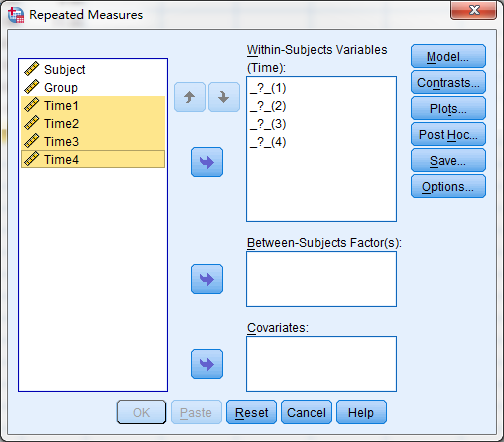
加入Within-subject variables
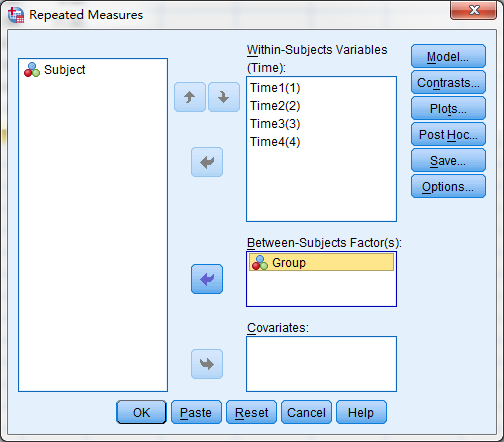
定义Between-subject factors
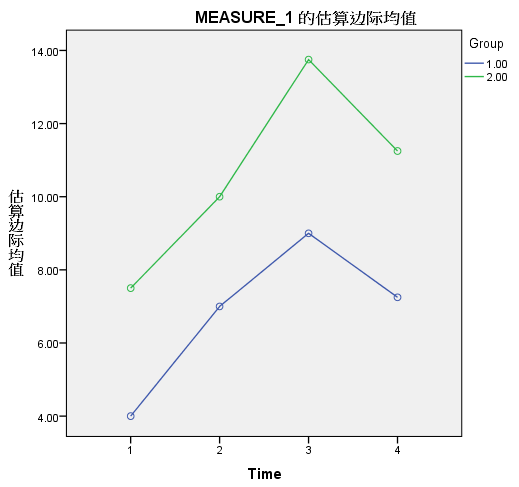
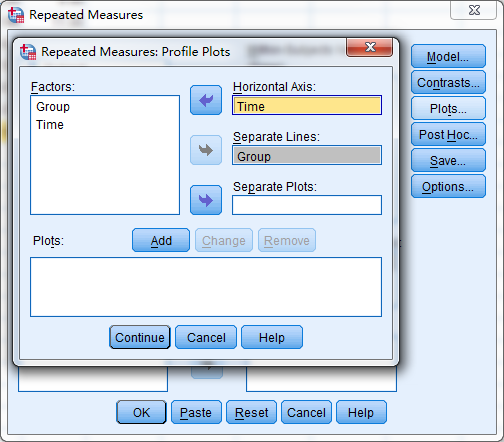
画边际均值图(plots)
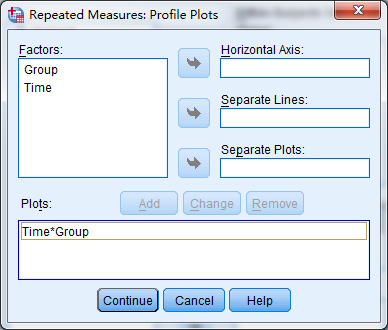
选择要输出的数据(opition)
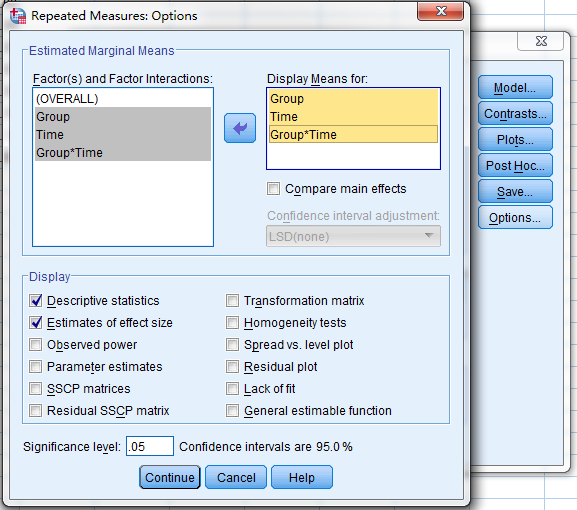
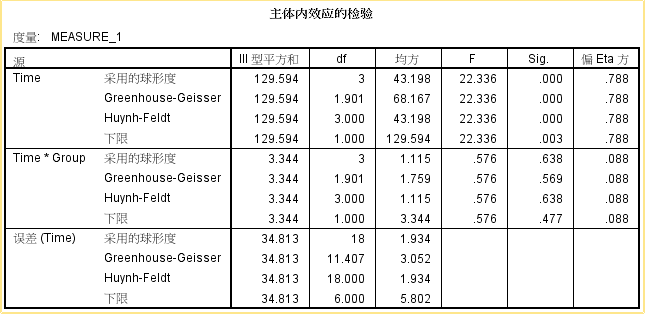
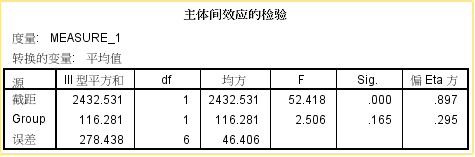
主效应及交互效应输出,及边际均值图,根据球形检验(Mauchly’s Test of Sphericity)的结果,如果p>0.05,说明数据符合球形假设条件,可按单因素方差分析方法处理;如果p<0.05,说明数据不符合球形假设条件,不能按单因素方差分析方法处理,宜用另外三种$\epsilon$校正方法Greenhouse-Geisser,Huynh-Feldt和Lower-bound对一元方差分析进行校正(对相应的F值进行校正)。